I must confess: I’ve always had some hesitation about writing on these topics. They’re too radical, too fundamental. One risks being taken for crazy. But for a couple of years now, one question has been pressing on me more insistently each day: are we really sure that space and time are the very backdrop on which the universe is built?
The answer is: it depends on the point of view. Surely, space and time are the constituents of the universe that our brain perceives through the five senses.
Up until the end of the 19th century, all phenomena were described within a three-dimensional world that had, at its center, a great clock: time.
Then special relativity taught us that space and time are not separate, but in some way bound together, belonging to a single entity called spacetime.

So, since the early 20th century, the stage on which physical phenomena occur has been spacetime. Today we take it for granted, even though at first it was difficult to accept that space and time are inseparable. Yet all experiments confirm exactly that.
Then came quantum mechanics. At first, we realized that we cannot know exactly where a particle is, but only with what probability we will find it at a certain point in space and time. This probability (or more precisely, probability density) is described by the wave function, the solution of Schrödinger’s equation.
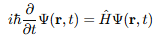
And according to the Copenhagen interpretation, the probability density function is precisely the squared modulus of the wave function (psi).

Up to this point, nothing too strange: we have a function that tells us with what probability we will find a particle at (x, y, z, t), in accordance with Born’s rule.
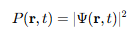
But upon a closer look, somethingweirdemerges: the particle doesn’t exist at any point in spacetime before it is measured or observed. So it’s not that the particle exists but we don’t know where it is—no, the particle does not exist at all in space and time!
At the moment of measurement, the wave function collapses into one of the possible eigenstates |aii>, secondo la cosiddetta proiezione:
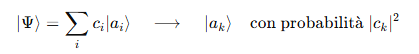
It is precisely in that moment that the particle acquires a position in spacetime.
And here the doubt arises: maybe the very question “where is a particle before measurement?” is a wrong question. What if spacetime doesn’t exist at the level of elementary particles? If spacetime doesn’t exist for an unobserved particle, then the question “where is it?” is meaningless—because “where” already assumes spacetime. And if spacetime itself doesn’t exist, the question collapses.
But when the particle is observed, spacetime most definitely exists. So, what does this mean?
Here’s the radical idea: spacetime is created at the moment of measurement—that is, at the moment of wave function collapse.
And the world we observe? In it, spacetime certainly exists. It’s as if there were “something” outside spacetime (I say outside because spacetime does not yet exist) that causes the wave functions of all particles to collapse, thereby creating spacetime. And I don’t mean that human observation makes wave functions collapse—that would be a huge misunderstanding. There is something that causes the collapse, but it certainly cannot live within spacetime (our world), because spacetime itself does not exist before the wave function collapse.
There is something that “unfolds” spacetime at the moment a property of a particle is observed or measured. The particle is then projected into spacetime. Spacetime, which we consider the fabric of the universe, is not the ultimate background of reality, but only the background after wave function collapse.
And before? The particle exists, but not in spacetime—it exists in another realm that does not rest on space and time. That is why space and time are not the fabric, the foundation, of the universe.
What this realm is, I don’t know. Nor do I know what exactly causes wave function collapse—I cannot describe it with equations, and that frustrates me. I’d be tempted to say that consciousness causes the collapse, but I don’t think we have a proper mathematical representation of consciousness—or at least, I don’t know one. Even though some authors have tried to translate consciousness into mathematical terms. Here are a few examples:
Von Neumann–Wigner: they speculated that consciousness is directly tied to wave function collapse. Today this interpretation is treated very cautiously, though it remains fascinating.
Integrated Information Theory (IIT, Tononi): consciousness is defined as the amount of integrated information, measured by a quantity called Φ.
Formally:
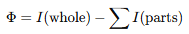
where I indicates information. It’s not a physics equation, but rather an attempt to give mathematical form to conscious experience.
Entropy-based relations: some propose that consciousness is tied to a system’s ability to reduce its uncertainty. Roughly:
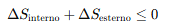
meaning that a conscious system would be one that optimally reorganizes internal and external entropy
I decided to write this article because I’ve noticed I’m not the only one thinking this “strange” way. Take a look at this…
Leave a Reply